一致性模型学习将扩散采样轨迹上的任何中间噪声数据点直接映射回其原点。由于同一轨迹上的任何数据点都映射到同一原点,因此它具有自一致性,因此被称为一致性模型(Consistency Model)。
1. Consistency Model
CM在Diffusion Model的基础上,新增了一个约束:从某个样本到某个噪声的加噪轨迹上的每一个点,都可以经过一个函数 $f$ 映射为这条轨迹的起点。 显然,同一条轨迹上的点经过 $f$ 的映射都是同一个点。这也是训练CM时所用到的损失约束。
当微调SD使其满足该性质之后,其采样过程就变成了:从噪声中采样一个点$z_T$,送入 $f$ 中,就得到了其对应的数据样本$z_0$,这就是CM的单步生成模式。同时,CM还可以通过多步生成来实现速度换质量的图片生成结果。具体来说,将单步得到的$z_0$经过Diffusion 模型的前向(加噪)过程得到$z_{t1}$ ,然后再从$z_{t1}$预测一个数据样本$z_0^{t1}$(表示经由$z_{t1}$得到的$z_0$)接着再加噪、预测$z_0$...如此循环就可以实现CM的多步采样生成。
原理解读
首先,我们需要明白,常用的Diffusion Model实际上是训练了一个网络$s_\phi(x,t)$ 来拟合$\nabla log(p_t(x))$,然后Diffusion的采样过程可以理解为给定$x_T \sim \mathbf{N(0,I)}$,有(EDM)
$$ \frac {dx_t} {dt} = -t s_\phi(x_t, t) $$
给定起始点,给定每个点的梯度后,通过迭代计算得到$x_\epsilon$ ,其中$\epsilon$ 是一个小正数(比如EDM中使用的0.002),用$x_\epsilon$作为采样得到的样本。(这里引入$\epsilon$是为了避免在$t=0$处出现数值不稳定的问题)。
Consistency在Diffusion的基础上,继续定义了一个一致性函数(Consistency function) $f: (x_t,t) \rightarrow x_\epsilon$ 。该函数有两个性质:
- 性质一:$f(x_\epsilon,\epsilon) = x_\epsilon$
- 性质二:任意$t_1,t_2 \in [\epsilon, T]$ 满足 $f(x_{t_1},t_1) = f(x_{t_2},t_2) = x_\epsilon$
CM的目标是找到一个$f_\theta$,能满足上这两个条件,来拟合$f$。之后,便可以使用下面的采样算法从高斯分布中进行采样。
性质一
参考EDM,CM直接设计$f_\theta(x,t)=c_{skip}(t)x+c_{out}F_\theta(x,t)$,边界条件$c_{skip}(\epsilon)=1$,$c_{out}(\epsilon)=0$,其中,
$$ c_{skip}(t)=\frac {\sigma_{data}^2} {(t-\sigma)^2+\sigma_{data}^2}, c_{out}(t)=\frac {\sigma_{data}(t-\epsilon)} {\sqrt{t^2+\sigma_{data}^2}} $$
需要注意的是,其中的$F_\theta(x,t)$就是给定$x_t$,$t$去预测一个$\hat x_0$。之前各种不同的Diffusion模型的预测结果都可以转变为预测$x_0$。由于$c_{skip}$很快收敛于0,$f_\theta(x,t)$其实基本由$F_\theta(x,t)$决定。显然,当$t=\epsilon$时,$f_\theta(x,t)$能满足一致性函数的第一条性质。
Wrong Wang在其博客中可视化了diffusers中LCM和CM的get_scalings_for_boundary_condition函数里的$c_{skip}$和$c_{out}$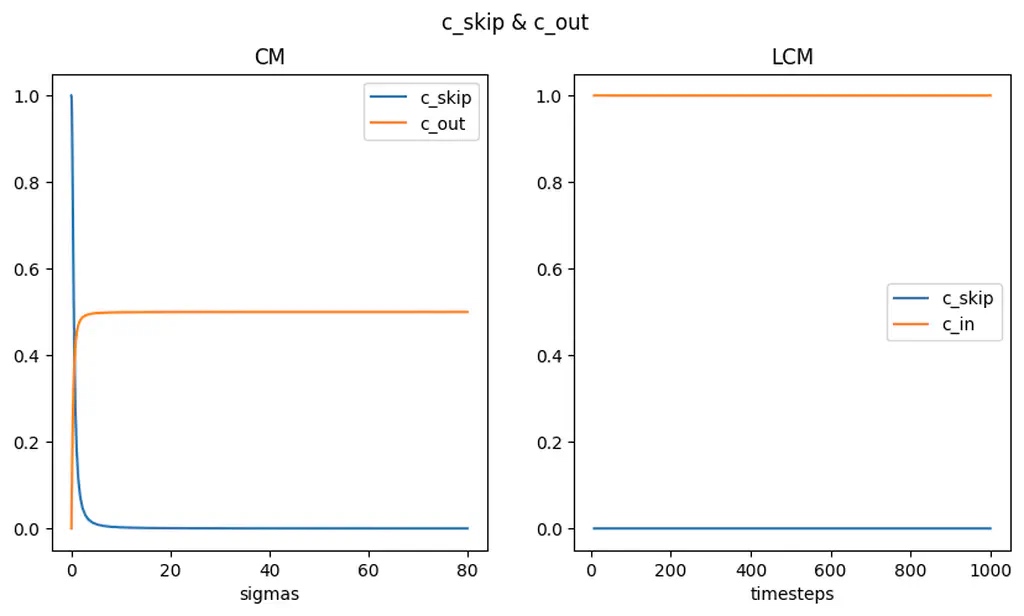
可以看到$c_{skip}$很快收敛于0,而LCM中直接令$\epsilon=0$。
性质二
可以通过最小化下面这个损失来拟合第二条性质:
$$ \mathcal{L}^N_\text{CD} (\theta, \theta^-; \phi) = \mathbb{E} [\lambda(t_n)d(f_\theta(\mathbf{x}_{t_{n+1}}, t_{n+1}), f_{\theta^-}(\hat{\mathbf{x}}^\phi_{t_n}, t_n)] $$
即将采样的$x_0$加噪变为$x_{t_{n+1}}$,然后利用Diffusion 模型去一次噪,预测到另外一个点$\hat{x}^\phi_{t_n}$。然后计算这两个点送入$f_\theta$后的结果,用特定损失函数约束其一致。
这里的预测过程用数学公式写就是,已知$s_\phi(x,t)$和$\frac {dx_t} {dt} = -t s_\phi(x_t, t)$,用ODE Solver $\Phi$ 去解这个ODE:
$$ \hat{\mathbf{x}}^\phi_{t_n} = \mathbf{x}_{t_{n+1}} - (t_n - t_{n+1}) \Phi(\mathbf{x}_{t_{n+1}}, t_{n+1}; \phi) $$
比如常用的Euler Solver就是$\Phi(\mathbf{x}_{t_{n+1}}, t_{n+1}; \phi)=-ts_\theta(x,t)$。DDIM、DPM++这些都是ODE Solver的一种。其中:
- $n \sim \mathcal{U}[1, N-1]$,服从$[1, N-1]$的均匀分布
网络参数$\theta^-$是EMA版本的 $\theta$,可以提升训练的稳定性,计算公式如下
$$ \theta^- \leftarrow \text{stopgard}(\mu\theta^-+(1-\mu)\theta), 0 \leq \mu \leq 1 $$
- $d(.,.)$是一个距离度量函数(作者考虑使用$l_1$和$l2$),$\forall \mathbf{x}, \mathbf{y}: d(\mathbf{x}, \mathbf{y}) \leq 0$,并且只有$\mathbf{x}=\mathbf{y}$的时候$d(\mathbf{x}, \mathbf{y})=0$
- $\lambda(.) \in \mathbb{R}^+$是一个正值加权函数,论文中设置$\lambda(t_n)=1$
模型的训练算法如下:
CM论文附录证明了,当最小化$\mathcal{L}^N_\text{CD} (\theta, \theta^-; \phi) $为0时,$f_\theta$和$f$的误差上确界足够小。所以只需要最小化$\mathcal{L}_{CD}^{N}$就能让 $f_\theta$ 满足第二条性质。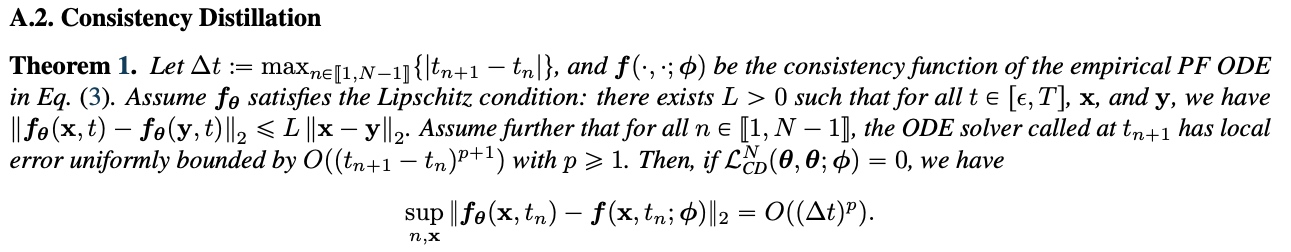
2. Latent Consistency Model
LCM是CM在文生图领域的一个应用,以CM作为理论基础,在一致性蒸馏的过程中引入了Classifier Free Guidance(CFG),也设计了skipping-step的策略来加速蒸馏收敛。
根据上文对CM的介绍,我们直接来看LCM具体的蒸馏过程:

其中蓝色部分为LCD相对于CD新增的部分。LCD比CD多了一个$\text{encoder}\space E(\cdot)$(VAE),多了一个CFG常用的Guidance Scale范围$[w_{min},w_{max}]$,以及一个表示Diffusion去噪过程中跳步大小的参数k。下面详细描述下LCD的蒸馏过程:
- 从数据集$\mathcal{D_z}$中采样$(z,c)$,即图片latent和对应的caption。在SD预训练模型中,$N=1000$,从$1$到$N-k$中采样当前训练所针对的timestep $n$,即从当前的sample$(z,c)$中选择了$z_{n+k},\hat z_n$这两个点去计算Consistency Loss。最后从$[w_{min},w_{max}]$中选一个$w$作为后续预测$\hat z_n$时使用的Guidance Scale。
- 加噪,用标准的DIffusion前向过程加噪得到$z_{n+k}$。
- 执行一次熟悉的Diffusion去噪过程,这一步融合了CFG的Guidance Scale得到$\hat{z}_{n}^{\Phi,w}$。
- 计算一致性蒸馏损失,通过对两个点:$z_{n+k}$和$\hat{z}_{n}^{\Phi,w}$,计算一致性函数输出,然后用一个损失函数约束输出一致。
- 更新网络权重。
- 计算网络EMA。
采样器和$k$的消融
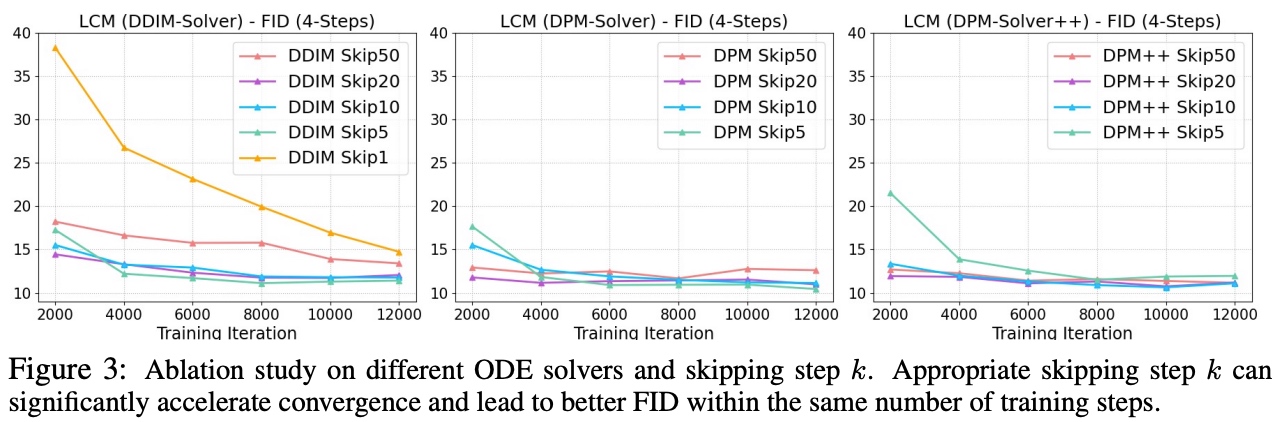
LCM对不同的ODE Solver和跳步大小$k$做了消融。当$k$足够合理时,只需要2000步迭代,LCM 4步采样的FID就已经基本收敛了。图DDIM-Solver中,当$k=1$时,收敛很慢,而$k=50$时,FID一直很高,说明$k$太大时,DDIM求解ODE误差太大,但此时对于其他采样器(DPM-Solver、DPM-Solver++)还是正常的。实验结果与采样器的效果时吻合的:$k=50$时,对应SD推理20步,此时DPM++和DPM的表现比DDIM要好。
CFG w取值的消融
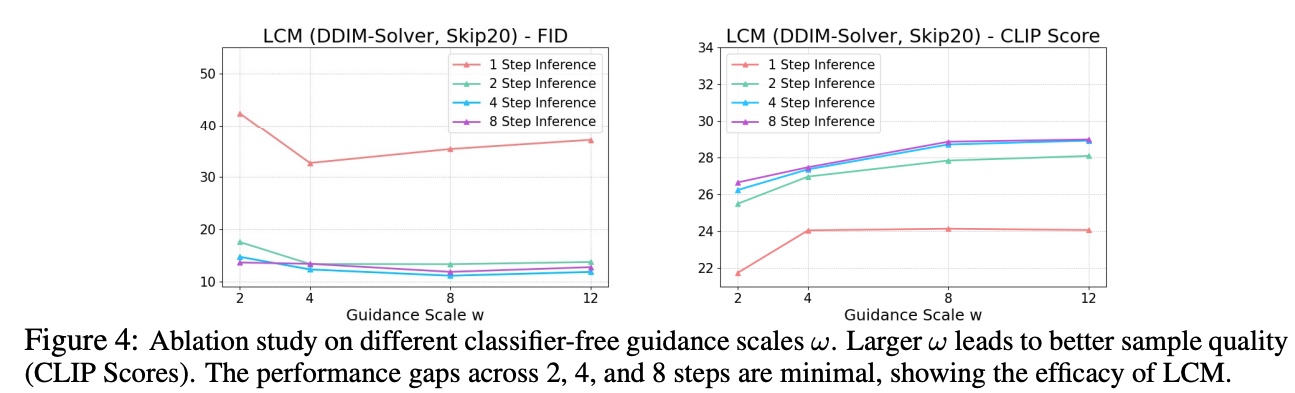
LCM作者使用不同的LCM推理步数与不同的Guidance Scale做对比。发现$w$的增加有助于提升CLIPScore,但是损失了FID指标(多样性)的表现。此外,LCM推理步数为2、4、8时,CLIP Score和FID相差都不大,说明LCM的蒸馏性能确实非常好。
3. LCM-LoRA
LCM-LoRA一经出世便引起了关注,其可以和现在开源社区各种LoRA模型组合的同时起到加速的效果。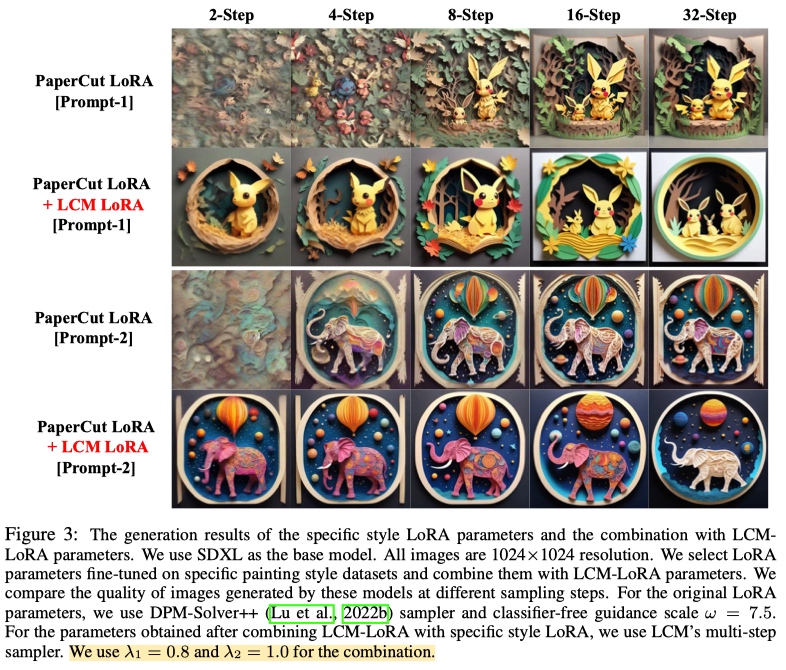

- 从模型角度出发,LoRA所做的事情为finetune低秩矩阵,不同LoRA之间进行加权冲突没那么大,因此可以进行混合。
- 从数据分布角度讲,微调过程中 Diffusion 前向的数据分布没有改变,顶多是子集的差异,LCM-LoRA依然用到了Diffusion去噪,且从$z_{n+k}$预测得到的$\hat{z}_n$依然接近真实$z_n$的分布。(引自wrong wang)
- 个人理解,LCM-LoRA的训练过程并没有破坏DIffusoin网络原有的训练目标,无非是在此基础上新增了一致性的损失,对$z_{n+k}$和$\hat{z}_{n}^{\Phi,w}$经过Diffusion降噪得到的结果进行约束。因此本质上,其可以看作是常规的LoRA训练。而LoRA之间的混合使用早已不是新鲜事,像mix-of-show,混合LoRA来达到组合概念生成的目的。
需要关注的是,由于LCM和LCM-LoRA在训练的过程中把CFG集成了进去,因此在推理时,不需要再去做CFG。